Affine Transformations of ROI Shapes

The OME Data Model defines a Shape.Transform element with an AffineTransform type that is used to transform a Shape’s position in the image in various ways: scaling, rotations and more. These transformations are performed within the two dimensions of the image’s x, y plane. In order to properly locate a Region of Interest (ROI) on an image any geometric transformations of its Shapes must be taken into account.

The OME Data Model transformation matrix

The OME Data Model’s AffineTransform defines the elements of a transformation matrix,

where the attributes’ geometric meaning is,

A00

scaling of x

A10

shearing of y

A01

shearing of x

A11

scaling of y

A02

translation of x

A12

translation of y

The accompanying graph shows an example translation of $\mathit{A02}=35$ in x and $\mathit{A12}=-65$ in y. The above representation of affine transformations reflects a common approach in computational geometry and works well.

ROI transformations in OMERO 5.2

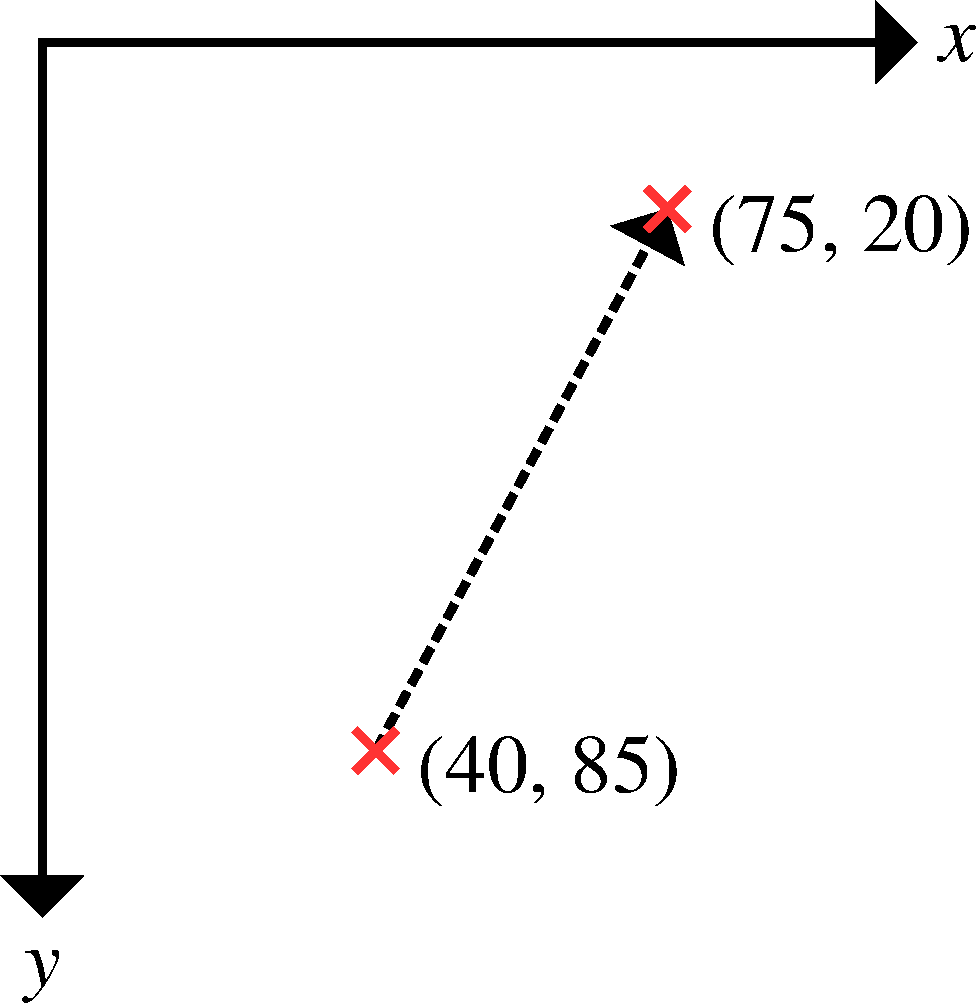
In OMERO 5.2 the Shape.transform property uses a single string to represent transformations. Historically a variety of formats have been used for this string, most from the World Wide Web Consortium’s Scalable Vector Graphics (SVG), anything from "none" to "rotate (12.000 262.000 174.000)". Unfortunately OMERO clients must thus bear the burden of parsing the possible string formats simply to be able to determine a ROI’s position on the image. From the example illustrated in the previous section, given a Point at (40, 85) with transform "translate(35 -65)", that Point should be understood to be located at (75, 20) in the image.

Parsed transformations in OMERO 5.3

The database upgrade script from OMERO 5.2 to 5.3 will include a parser written in PL/pgSQL that moves these string-based Shape.transform property values of existing ROIs to a new OMERO model object, AffineTransform, whose properties mirror the numeric attributes of the corresponding OME-XML element.

From OMERO 5.3 a Shape that does have an associated transform thus has the named matrix elements A00, A10, A01, A11, A02, A12 conveniently available to OMERO clients as floating-point numbers. This makes it far easier to write clients that properly take account of how a ROI’s Shapes have been transformed.

Adapting existing code

The OME Data Model and Bio-Formats remain unchanged in regard to affine transformations. However, the above constitutes a breaking change for OMERO users. We do not make such changes lightly.

It is highly likely that existing client code that works with OMERO 5.2’s SVG-based Shape.transform property strings already translates them to fit the properties of the new OMERO AffineTransform model object. Such code may parse the "matrix(a00, a10, a01, a11, a02, a12)" SVG format or use transformation matrices in its actual calculation or display. For example, in adapting some of our Java code for OMERO 5.3 we found that the AffineTransform object’s properties directly correspond to properties of the AWT’s AffineTransform Java class that we use already. We are therefore optimistic that, while some ROI-related code does have to be adjusted, it will be a relatively easy process that leaves the code clearer and simpler.